개요
정렬은 실행하는 방법에 따라 두 가지로 나눌 수 있다.
비교식 정렬 은 한 번에 두 개씩 비교하여 교환하여 정렬하는 방식이고,
분배식 정렬 은 키값을 기준으로 자료를 여러 개의 부분집합으로 분해하고 부분집합을 정렬함으로써 전체를 정렬하는 방식이다.
| 종류 | 설명 | 예시 |
|---|---|---|
| 교환 방식 | 키를 비교하고 교환하여 정렬하는 방식 | 선택 정렬, 버블 정렬, 퀵 정렬 |
| 삽입 방식 | 키를 비교하고 삽입하여 정렬하는 방식 | 삽입 정렬, 셸 정렬 |
| 병합 방식 | 키를 비교하고 병합하여 정렬하는 방식 | 2-way 병합, n-way 병합 |
| 선택 방식 | 이진 트리를 사용하여 정렬하는 방식 | 힙 정렬, 트리 정렬 |
| 분배 방식 | 키를 구성하는 값을 여러 개의 부분집합에 분배하여 정렬하는 방식 | 기수 정렬 |
이 포스트에서는 비교식 정렬 중 선택 정렬, 삽입 정렬, 버블 정렬에 대하여 다룬다.
시간 복잡도는 모두 \(O(n^2)\)이다.
1. 선택 정렬
선택 정렬이란
선택 정렬(Selection Sort)은 전체 원소 중에서 현재 위치에 맞는 원소를 찾아 자리를 교환하는 방식을 반복하여 정렬한다.
- 동일한 값에 대해 기존의 순서가 유지되지 않는 불안정 정렬이다.
- 정렬하고자 하는 배열 안에서 정렬이 수행되는 제자리 정렬이다.
(1) 전체 원소 중 첫번째 로 작은 원소를 찾아 자리 교환
(2) 전체 원소 중 두번째 로 작은 원소를 찾아 자리 교환
…
(n) 전체 원소 중 n번째 로 작은 원소를 찾아 자리 교환
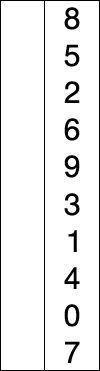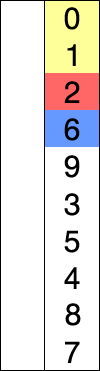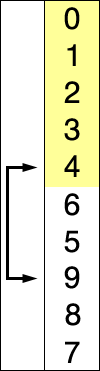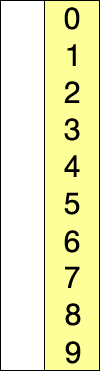
Pseudo Code
selectionSort(a[], n)
for(i←1; i<n; i←i+1) do {
a[i], ... , a[n-1] 중에서 가장 작은 원소 a[k]를 선택해 a[i]와 교환
}
end selectionSort()
시간 복잡도
(1) 첫번째 원소와 n-1 개 원소 비교
(2) 두번째 원소와 n-2 개 원소 비교
…
(i) i번째 원소와 n-i 개 원소 비교
…
(n) 마지막 원소와 1 개 (자기 자신) 원소 비교
- 전체 비교 횟수 : \((n-1)+(n-2)+...+2+1=\sum_{i=1}^{n-1} {n-i} =\frac{n(n-1)}{2}\)
- 시간 복잡도 : \(O(n^2)\)
2. 삽입 정렬
삽입 정렬이란
삽입 정렬(Insertion Sort)은 정렬할 원소가 들어갈 위치를 찾아 해당 위치에 원소를 삽입하는 방식이다. 삽입 정렬에서는 정렬할 자료가 정렬된 부분집합 (S; Sorted Subset)과 정렬되지 않은 부분집합 (U; Unsorted Subset)으로 나뉘어 있다고 가정한다. 삽입 정렬을 수행할 때마다 S 의 원소는 하나씩 늘어나고, U 의 원소는 하나씩 줄어든다.
- 동일한 값에 대해 기존의 순서가 유지되는 안정 정렬이다.
- 정렬하고자 하는 배열 안에서 정렬이 수행되는 제자리 정렬이다.
(0) 첫번째 원소는 S내에 이미 정렬되어 있음
(1) 두번째 원소(U의 첫번째 원소)의 정렬될 위치(S 내)를 찾아 해당 위치에 삽입
(2) 세번째 원소(U의 첫번째 원소)의 정렬될 위치(S 내)를 찾아 해당 위치에 삽입
…
(n) n번째 원소(U의 첫번째 원소)의 정렬될 위치(S 내)를 찾아 해당 위치에 삽입
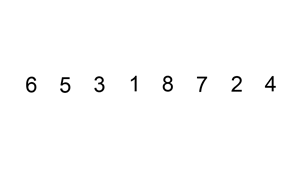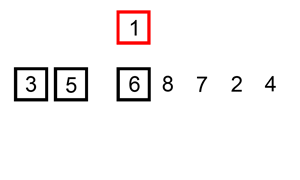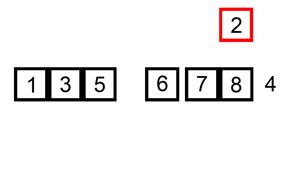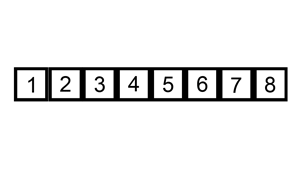
Pseudo Code
insertionSort(a[], n)
for(i←1; i<n; i←i+1) do {
temp ← a[i];
j ← i;
if(a[j-1]>temp) then move ← true;
else move ← false;
while(move and j>0) do {
a[j] ← a[j-1];
j ← j-1;
}
a[j] ← temp;
}
시간 복잡도
(1) 최선의 경우(순차 정렬된 경우)
- 전체 비교 횟수 : \(n-1\)
- 전체 자리 이동 횟수 : \(0\)
- 시간 복잡도 : \(O(n)\)
(2) 최악의 경우(역순 정렬된 경우)
- 전체 비교 횟수 : \(1+2+3+...+(n-1) = \sum_{i=1}^{n-1} {i}\)
- 전체 자리 이동 횟수 : \(1+2+3+...+(n-1) = \sum_{i=1}^{n-1} {i}\)
- 실행 연산 횟수 : \(\sum_{i=1}^{n-1} {i+i}\)
- 시간 복잡도 : \(O(n^2)\)
따라서 평균 시간 복잡도 는 \(O(n^2)\)이다.
3. 버블 정렬
버블 정렬이란
버블 정렬(Bubble Sort)은 인접한 원소를 두 개 비교하여 자리를 교환하는 방식을 반복하여 정렬한다. 버블 정렬을 수행하면 큰 원소가 가장 끝으로 이동하게 되므로 자료의 끝부터 정렬된다.
- 동일한 값에 대해 기존의 순서가 유지되는 안정 정렬이다.
- 정렬하고자 하는 배열 안에서 정렬이 수행되는 제자리 정렬이다.
(1) 인접한 원소끼리 비교, 첫번째로 큰 원소가 정렬됨 (가장 끝인 n번째에 위치)
(2) 인접한 원소끼리 비교, 두번째로 큰 원소가 정렬됨 (n-1번째에 위치)
…
(n) 마지막으로 큰 원소가 정렬됨 (첫번째에 위치)
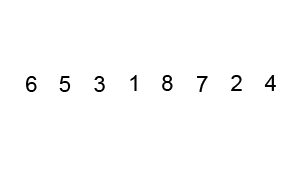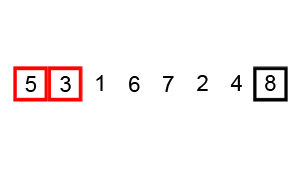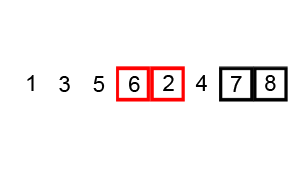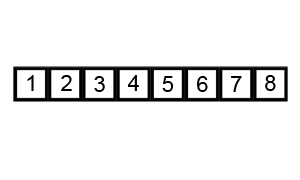
Pseudo Code
bubbleSort(a[], n)
for(i←n-1; i>=0; i←i-1) do {
for(j←0; j<i; j←i+1) do {
if(a[j]>a[j+1]) then {
temp ← a[j];
a[j] ← a[j+1];
a[j+1] ← temp;
}
}
}
end bubbleSort()
시간 복잡도
(1) 최선의 경우(순차 정렬된 경우)
- 전체 비교 횟수 : \(1+2+3+...+(n-1)=\sum_{i=1}^{n-1} {i} =\frac{n(n-1)}{2}\)
- 전체 자리 이동 횟수 : \(0\)
- 시간 복잡도 : \(O(n^2)\)
(2) 최악의 경우(역순 정렬된 경우)
- 전체 비교 횟수 : \(1+2+3+...+(n-1)=\sum_{i=1}^{n-1} {i} =\frac{n(n-1)}{2}\)
- 전체 자리 이동 횟수 : \(1+2+3+...+(n-1)=\sum_{i=1}^{n-1} {i} =\frac{n(n-1)}{2}\)
- 시간 복잡도 : \(O(n^2)\)
따라서 평균 시간 복잡도 는 \(O(n^2)\)이다.
REFERENCE
C로 배우는 쉬운 자료구조 - 개정 3판, 이지영
Insertion sort
Selection sort
Bubble sort
[알고리즘] - 선택 정렬(Selection sort) #5