개요
정렬은 실행하는 방법에 따라 두 가지로 나눌 수 있다.
비교식 정렬 은 한 번에 두 개씩 비교하여 교환하여 정렬하는 방식이고,
분배식 정렬 은 키값을 기준으로 자료를 여러 개의 부분집합으로 분해하고 부분집합을 정렬함으로써 전체를 정렬하는 방식이다.
| 종류 | 설명 | 예시 |
|---|---|---|
| 교환 방식 | 키를 비교하고 교환하여 정렬하는 방식 | 선택 정렬, 버블 정렬, 퀵 정렬 |
| 삽입 방식 | 키를 비교하고 삽입하여 정렬하는 방식 | 삽입 정렬, 셸 정렬 |
| 병합 방식 | 키를 비교하고 병합하여 정렬하는 방식 | 2-way 병합, n-way 병합 |
| 선택 방식 | 이진 트리를 사용하여 정렬하는 방식 | 힙 정렬, 트리 정렬 |
| 분배 방식 | 키를 구성하는 값을 여러 개의 부분집합에 분배하여 정렬하는 방식 | 기수 정렬 |
이 포스트에서는 비교식 정렬 중 퀵 정렬, 병합 정렬, 힙 정렬에 대하여 다룬다.
시간 복잡도는 모두 \(O(nlog_2 n)\)이다.
1. 퀵 정렬
퀵 정렬이란
퀵 정렬(Quick Sort)은 기준값(피봇; Pivot)을 중심으로 자료를 왼쪽 부분집합과 오른쪽 부분집합으로 분할한다. 왼쪽 부분집합으로 기준값보다 작은 원소를 이동시키고, 오른쪽 부분집합으로 기준값보다 큰 원소를 이동시킨다.
퀵 정렬(Quick Sort)은 분할과 정복(Divide and Conquer)라는 작업을 반복하여 수행한다.
- 동일한 값에 대해 기존의 순서가 유지되지 않는 불안정 정렬이다.
(1) 왼쪽 끝에서 오른쪽으로 움직이면서 피봇보다 크거나 같은 원소를 찾아 L로 표시
(2) 오른쪽 끝에서 왼쪽으로 움직이며 피봇보다 작은 원소를 찾아 R로 표시
(3) L과 R을 서로 교환하고 (1) 과 (2) 를 반복 수행
(4) L과 R이 만나는 경우 멈추고 R과 피봇의 원소를 교환
(5) 피봇을 다시 정하고 (1) ~ (2) 반복
(6) 모든 부분집합의 크기가 1 이하가 되면 퀵 정렬 종료
Pseudo Code
quickSort(a[], begin, end){
if (m < n) then{
p ← partition(a, begin, end);
quickSort(a[], begin, p-1);
quickSort(a[], p+1, end);
}
}
end quickSort()
partition(a[], begin, end){
pivot ← (begin + end) / 2;
L ← begin;
R ← end;
while (L < R) do {
while (a[L] < a[pivot] and L<R) do L++;
while (a[R] >= a[pivot] and L<R) do R--;
if(L < R) then {
temp ← a[L];
a[L] ← a[R];
a[R] ← temp;
}
}
temp ← a[pivot];
a[pivot] ← a[R];
a[R] ← temp;
return R;
}
end partition()
시간 복잡도
(1) 최선의 경우
- 피봇에 의한 원소들의 부분집합이 정확히 n/2개씩 2등분 되는 경우가 반복되는 경우
- 시간 복잡도 : \(O(nlog_2 n)\)
(2) 최악의 경우
- 피봇에 의한 원소들의 부분집합이 1개과 n-1개로 분할되는 경우가 반복되는 경우
- 시간 복잡도 : \(O(n^2)\)
따라서 평균 시간 복잡도 는 \(O(nlog_2 n)\)이다.
공간 복잡도
주어진 배열 내에서 교환을 하며 수행하므로 \(O(n)\)이다.
2. 병합 정렬
병합 정렬이란
병합 정렬(Merge Sort)은 여러 개의 정렬된 집합을 병합하여 하나의 정렬된 집합으로 만드는 정렬 방법이다. 자료를 부분집합으로 분할 하고 부분집합에 대해 작업을 정복 하고 부분집합들을 다시 결합 하는 분할과 정복(Divide and Conquer) 방법을 사용한다.
병합 정렬은 순차적인 비교를 통해 정렬하므로, LinkedList의 정렬에 효율적이다.
- 동일한 값에 대해 기존의 순서가 유지되는 안정 정렬이다.
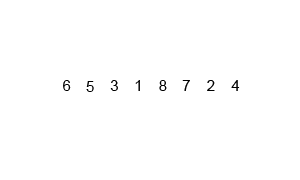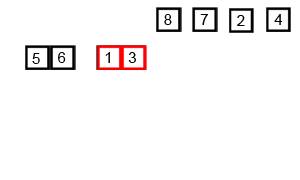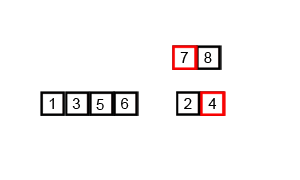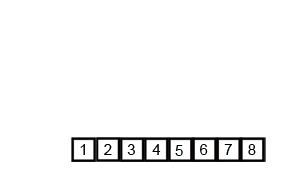
Pseudo Code
mergeSort(a[], m, n){
if(a[m:n]의 원소 수 > 1) then {
전체 집합을 부분집합 두 개로 분할;
}
mergeSort(a[], m, middle);
mergeSort(a[], middle+1, n);
merge(a[m:middle], a[middle+1:n]);
}
end mergeSort()
merge(a[m:middle], a[middle+1:n]){
i ← m;
j ← middle + 1;
k ← m;
while(i<=middle and j<=n) do {
if(a[i] <= a[j]) then {
sorted[k] ← a[i];
i ← i + 1;
}
else {
sorted[k] ← a[j];
j ← j + 1;
}
k ← k + 1;
}
if(i > middle) 두 번째 부분집합에 남아 있는 원소를 sorted에 복사;
else 첫 번째 부분집합에 남아 있는 원소를 sorted에 복사;
}
end merge()
복잡도
- 공간 복잡도 : 원래의 자료 n개에 대해 정렬할 원소를 저장할 2*n개 의 추가공간 필요
-
시간 복잡도
- 분할 : n개 원소를 두 개로 분할 -> \(O(log_2 n)\)
- 병합 : 최대 n번의 비교 연산 -> \(O(n)\)
- 따라서 시간 복잡도는 \(O(nlog_2 n)\)이다.
3. 힙 정렬
힙 정렬이란
힙 정렬(Heap Sort)은 Heap 자료구조를 이용해 정렬하는 방법이다. 최대 히프 에서 원소 개수만큼 삭제 연산을 수행하면 내림차순으로 정렬된 원소를 얻을 수 있고, 최소 히프 에서 원소 개수만큼 삭제 연산을 수행하면 오름차순으로 정렬된 원소를 얻을 수 있다는 성질을 이용한다.
- 동일한 값에 대해 기존의 순서가 유지되지 않는 불안정 정렬이다.
(1) 정렬할 원소에 대해 삽입 연산을 통해 최대 히프 구성
(2) 최대 히프 에서 삭제 연산하여 배열의 비어있는 자리 중 마지막 자리에 저장
(3) 남은 히프를 최대 히프 로 재구성
(4) 공백 히프가 될 때 까지 (2) ~ (3) 반복

Pseudo Code
heapSort(a[]){
n ← a.length - 1;
for(i ← n/2 ; i >= 1 ; i ← i - 1)
makeHeap(a, i, n);
for(i ← n/2 ; i >= 1 ; i ← i - 1) {
temp ← a[1];
a[1] ← a[i+1];
a[i+1] ← temp;
makeHeap(a, 1, i);
}
}
end heapSort()
makeHeap(a[], h, m){
for(j ← 2*h ; j <= m ; j ← 2*j){
if(j < m)
if(a[j]<a[j+1]) j ← j + 1;
if(a[h] >= a[j]) then exit;
else a[j/2] ← a[j];
}
a[j/2] ← a[h];
}
end makeHeap()
복잡도
- 공간 복잡도 : 원래의 자료 n개에 대해 n개의 메모리 와 n개의 원소를 담을 수 있는 히프 추가 필요
-
시간 복잡도
- 정렬된 원소 구하기(히프 재구성) : 완전 이진 트리를 히프로 구성하는 평균 시간 \(O(log_2 n)\)
- n개 노드에 대해 삭제 연산한 히프 재구성 시간 : \(O(nlog_2 n)\)
- 따라서 시간 복잡도는 \(O(nlog_2 n)\)이다.
REFERENCE
C로 배우는 쉬운 자료구조 - 개정 3판, 이지영
Merge sort
Heapsort
Quicksort
